So, let’s first set some expectations straight: this topic is not about predicting the group size at distance, nor about terminal performance etc. It is about predicting the distance where the danger zone of (self-)destabilization of pellets will start. For those who follow me on instagram might have already seen this topic pass their feed a couple times in the past year:
First post: https://www.instagram.com/p/COa_To4BvlG/ (keep in mind that not all of it is perfectly explained, it’s a topic that is still being studied and I had to start somewhere ).
).
Matt Dubber, Ted Bier and some others have done a great job in identifying factors which have an influence on stability of pellets.
Despite that I was still missing an explanation of what and when it happens down range. @bushwacker and I were both thinking about this and by combining experiences of testing a lot of different pellets (and slugs) with some theories we came up with something. The goal was to be able to predict the maximum effective distance of a pellet before it gets into the danger zone of instability.
After monitoring a lot of spiralling of different pellets at long distances we started looking for variables to predict the instability. Let’s start breaking down of what is investigated to find a relation:
Let’s dive a bit more into what we see:
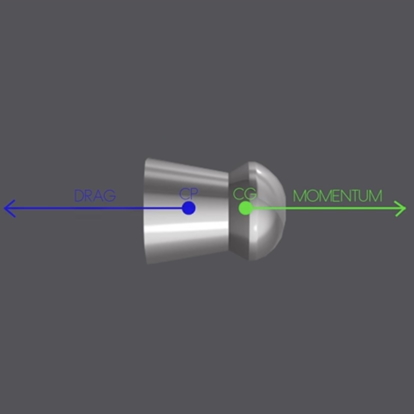
The picture above is important for understanding what is happening. During stable flight the centre of pressure (CP) is behind the centre of gravity (CG) for flare stabilized projectiles (yes you read it correctly; pellets are flare stabilized, not drag stabilized ). What is important here is that the centre of pressure (CP) stays behind the centre of gravity (CG) with a certain margin. Think of it like this: the centre of pressure (CP) varies during the flight; it moves inwards towards the front of the pellet while it’s slowing down, and at a certain point the CP and CG (centre of gravity) reach a position where the ratio between the pellet’s rotational inertia (combination of spin rate and weight distribution along the radius), forward momentum and CP-CG margin becomes critical. Combine that with the weight distribution of a pellet, which is the skirt weight attached to the head weight via the small waist -> roughly said a dumbbell weight distribution. Taking all of this into account to try to answer the following question: do pellets have a (self-inflicting) destabilization at some point which is either easily triggered by an outside force or can start by itself. And most important: how to predict this point or range?
). What is important here is that the centre of pressure (CP) stays behind the centre of gravity (CG) with a certain margin. Think of it like this: the centre of pressure (CP) varies during the flight; it moves inwards towards the front of the pellet while it’s slowing down, and at a certain point the CP and CG (centre of gravity) reach a position where the ratio between the pellet’s rotational inertia (combination of spin rate and weight distribution along the radius), forward momentum and CP-CG margin becomes critical. Combine that with the weight distribution of a pellet, which is the skirt weight attached to the head weight via the small waist -> roughly said a dumbbell weight distribution. Taking all of this into account to try to answer the following question: do pellets have a (self-inflicting) destabilization at some point which is either easily triggered by an outside force or can start by itself. And most important: how to predict this point or range?
By looking at pictures and easily available numbers the problem couldn’t be solved. So, what do you start doing as a curious engineer which refuses to believe this behaviour is random or unpredictable: start crunching numbers until a relation can be found .
.
I’ve made a sheet to start the crunching:
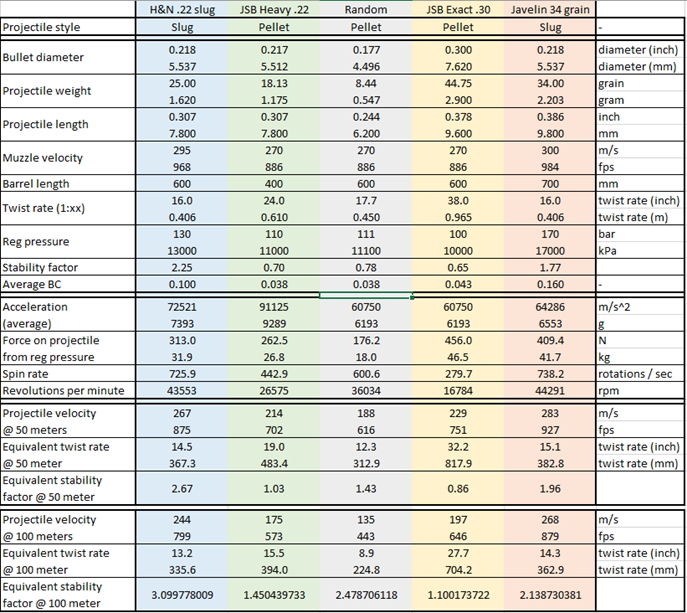
I started out with a mix of pellets and slugs to see if a relation could be established but that ended quite quickly. From gut feeling we knew it must have something to do with the downrange stabilisation, but it took me some time to find a relation there.
By using some reverse engineering from the observed data while pellet testing and linking it to the downrange equivalent stability factor progress started to appear. In this sheet you can see that the stability factor increases over distance (read it ‘stabilises’ more in the case of slugs and bullets) but it will show that this is actually a very important number (not specifically in a way you would expect).
After a lot of number crunching, re-adjusting theories and expectations, the result started showing that there seems to be a relation between the dimensions of the pellet and a certain downrange equivalent stability factor. Around a certain value of this downrange stability factor (and thus a downrange velocity) pellets start to spiral or just need a slight or sudden push from the wind to start spiralling. Since I couldn’t find an exact number at which this starts to happen, because it’s not a case of slowing down that 1 m/s (or fps) and suddenly it’s out of control, I would prefer to call it entering the danger zone. The danger zone is the dowrange velocity zone where there is a high risk of self-destabilisation or with the slightest stimulus it goes out of control.
Some assumptions that had to be made to keep it sort of simple:
Now, where can we use this info for: I’ve put all my formulas in Matlab (nerd program for mathematics) to solve the formulas for me.
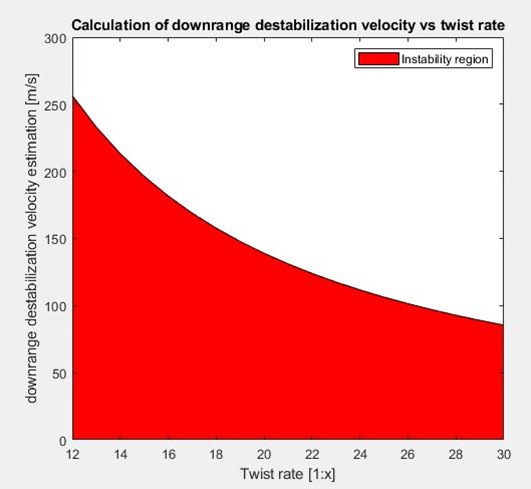
This curve shows what the downrange destabilization velocity estimation is vs the twist rate of the barrel for the 18.1 grain JSB Heavy in .22 at 275 m/s at 20 degrees Celsius. As soon as the downrange velocity of the pellet goes into the red area of the graph it is in the danger zone for destabilization. When I run these numbers through a ballistics calculator it can be translated to actual distances:
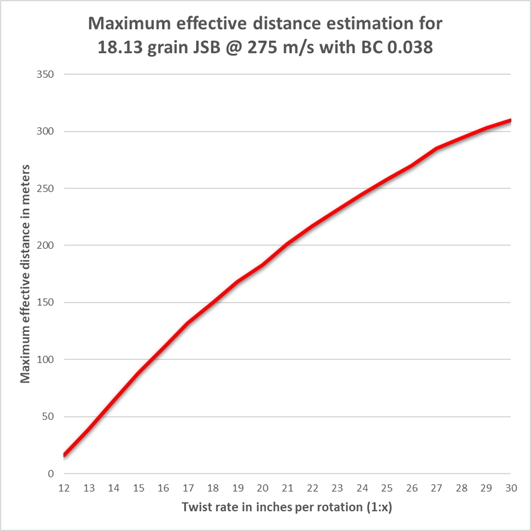
A conclusion that can be drawn from these graphs is that slow twists help in long range performance for pellets by delaying the self-destabilization.
Funny thing: slugs/bullets need a minimum stability Sg value of 1.5 to expect maximum BC to be reached and to be gyroscopically stable, with pellets the exact opposite behaviour is seen. Pellets seem to have a maximum downrange equivalent stability number at which they are expected to remain stable.
I can run these numbers for basically any pellet. To verify the theory, we’ve compared the numbers to observations, and it seems to match quite accurately but some finetuning is still required. I’m also working on writing a program which allows this theory to be used by basically anyone, but this will take some time.
Disclaimer, this is still just a theory which I wanted to share but I’m looking for more data to verify the validity. So predictions can be made but don’t shoot the messenger if your experience deviates slightly from the numbers. Feel free to think along, input is welcome
First post: https://www.instagram.com/p/COa_To4BvlG/ (keep in mind that not all of it is perfectly explained, it’s a topic that is still being studied and I had to start somewhere
Matt Dubber, Ted Bier and some others have done a great job in identifying factors which have an influence on stability of pellets.
Despite that I was still missing an explanation of what and when it happens down range. @bushwacker and I were both thinking about this and by combining experiences of testing a lot of different pellets (and slugs) with some theories we came up with something. The goal was to be able to predict the maximum effective distance of a pellet before it gets into the danger zone of instability.
After monitoring a lot of spiralling of different pellets at long distances we started looking for variables to predict the instability. Let’s start breaking down of what is investigated to find a relation:
- One of the first that comes up is downrange velocity. This wasn’t consistent enough to solely use for predicting it since there is a difference with varying twist rates and muzzle velocities. Read: there was not just a fixed downrange velocity at where it starts to spiral.
- twist rate: same idea as mentioned at downrange velocity.
- Pellet itself: length, weight, etc. No straightforward conversion factor or whatever to find a relation between the destabilization distance/velocity and the sizes of the pellet.
- Gyroscopic stability factor: this one is a bit tricky because it in most cases only tells you something about what happens at the muzzle. Add to that that the standard stability formulas are not made for pellet shapes.
- Ballistic coefficient: also, no straightforward conversion factor or ratio could be translated to the observations.
- Spin rate: this is the relation between muzzle velocity and twist rate and gives the rpm value of your projectile. Also, no direct relations here.
Let’s dive a bit more into what we see:
The picture above is important for understanding what is happening. During stable flight the centre of pressure (CP) is behind the centre of gravity (CG) for flare stabilized projectiles (yes you read it correctly; pellets are flare stabilized, not drag stabilized
By looking at pictures and easily available numbers the problem couldn’t be solved. So, what do you start doing as a curious engineer which refuses to believe this behaviour is random or unpredictable: start crunching numbers until a relation can be found
I’ve made a sheet to start the crunching:
I started out with a mix of pellets and slugs to see if a relation could be established but that ended quite quickly. From gut feeling we knew it must have something to do with the downrange stabilisation, but it took me some time to find a relation there.
By using some reverse engineering from the observed data while pellet testing and linking it to the downrange equivalent stability factor progress started to appear. In this sheet you can see that the stability factor increases over distance (read it ‘stabilises’ more in the case of slugs and bullets) but it will show that this is actually a very important number (not specifically in a way you would expect).
After a lot of number crunching, re-adjusting theories and expectations, the result started showing that there seems to be a relation between the dimensions of the pellet and a certain downrange equivalent stability factor. Around a certain value of this downrange stability factor (and thus a downrange velocity) pellets start to spiral or just need a slight or sudden push from the wind to start spiralling. Since I couldn’t find an exact number at which this starts to happen, because it’s not a case of slowing down that 1 m/s (or fps) and suddenly it’s out of control, I would prefer to call it entering the danger zone. The danger zone is the dowrange velocity zone where there is a high risk of self-destabilisation or with the slightest stimulus it goes out of control.
Some assumptions that had to be made to keep it sort of simple:
- To calculate the stability factor I used the Miller theorem, I know this is not made for pellets but at least it works as a solid base in these calculations.
- Spin rate is an important factor to calculate downrange twist rate equivalent for using it in the Miller theorem. During flight the spin rate decreases but this was very difficult to predict. I’ve asked Applied Ballistics (Bryan Litz his company), they said they were going to look into it but no response yet.
Now, where can we use this info for: I’ve put all my formulas in Matlab (nerd program for mathematics) to solve the formulas for me.
This curve shows what the downrange destabilization velocity estimation is vs the twist rate of the barrel for the 18.1 grain JSB Heavy in .22 at 275 m/s at 20 degrees Celsius. As soon as the downrange velocity of the pellet goes into the red area of the graph it is in the danger zone for destabilization. When I run these numbers through a ballistics calculator it can be translated to actual distances:
A conclusion that can be drawn from these graphs is that slow twists help in long range performance for pellets by delaying the self-destabilization.
Funny thing: slugs/bullets need a minimum stability Sg value of 1.5 to expect maximum BC to be reached and to be gyroscopically stable, with pellets the exact opposite behaviour is seen. Pellets seem to have a maximum downrange equivalent stability number at which they are expected to remain stable.
I can run these numbers for basically any pellet. To verify the theory, we’ve compared the numbers to observations, and it seems to match quite accurately but some finetuning is still required. I’m also working on writing a program which allows this theory to be used by basically anyone, but this will take some time.
Disclaimer, this is still just a theory which I wanted to share but I’m looking for more data to verify the validity. So predictions can be made but don’t shoot the messenger if your experience deviates slightly from the numbers. Feel free to think along, input is welcome
