One thing which affects all shooters, but in particular the air gun shooter, is the effect of a cross wind giving downwind drift. Here I will try to explain in a simple way how downwind drift is produced and how it varies with range and speed so that readers may understand better how their pellets are affected. I will not look at the vertical effect of a cross wind as that is much more complicated, but I will say that contrary to popular myth it is not due to Magnus.
When a pellet is fired in the air, as everyone knows, it slows down. To reach a certain range from the gun, because it slows down, it will take longer to reach that range than it would have done if it had just kept on going at the same speed. Because the pellet starts to slow down almost immediately after it has left the barrel, it will always take longer to travel a certain range, no matter how large or small the chosen distance is.
Suppose we choose a fixed range, say 30 yards, and a .22 pellet with a muzzle velocity of 585ft/sec. To reach 30 yards, that pellet will take 0.1635 seconds (AA Field pellet). Now if that pellet did not slow down at all but just kept on going at the same speed it would take 0.1538 seconds to travel 30 yards, so we can say that in the air it takes 0.0097 seconds longer to travel 30 yards than it would have done if it had kept going at the same speed. This time difference, the 0.0097 seconds, is called the lag time. The downwind drift at 30 yards for our pellet fired in the air is then given by the cross wind speed multiplied by that time difference. So in our case, for a 5mph cross wind, which is the same as a 88inches/sec cross wind, the downwind drift will be 0.0097 X 88 which comes out to 0.8536 inches. But the question is, why is downwind drift dependent on how much the pellet slows down?
The most popular misconception is that a crosswind blows on the side of a pellet. It is not surprising that this myth is popular, before now I have seen it written down in magazines, stated in videos and on forums. The wind will not blow on the side of the pellet if the pellet is stable (unless the pellet is grossly gyroscopically over stable, in which case you will have much more than a cross wind to worry about). A stable pellet, by definition, will always turn to face the direction from which the air is coming when it meets the front of the pellet. If there is no cross wind, the only thing giving a direction for the air to come from is the pellets own speed as it moves through the air, so the pellet will face in that direction.
When there is a cross wind, the air direction is not just due to the pellet speed. There is also the wind speed to think of. The pellet though does not see two separate wind directions, it sees a combination of the directions of the cross wind speed and the wind speed from the pellets own movement creating a relative airflow. Again, by the definition of a stable pellet, the pellet will turn to face the direction of the relative air flow from the cross wind and the pellet speed. The diagram below shows what is happening.
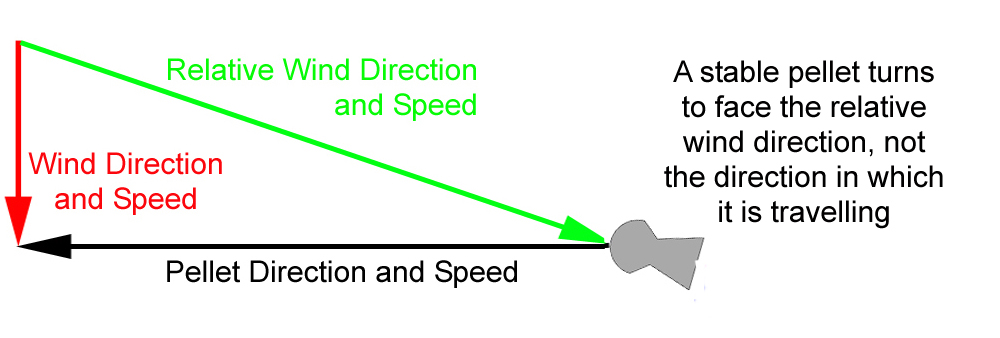
If the pellet is facing into the combined relative airflow, then there cannot be any flow on the side of the pellet to push it sideways down wind.
Since the pellet is facing the airflow, the only force acting on it is drag, and it is part of the drag force which produces the downwind drift. The next diagram shows how this happens.
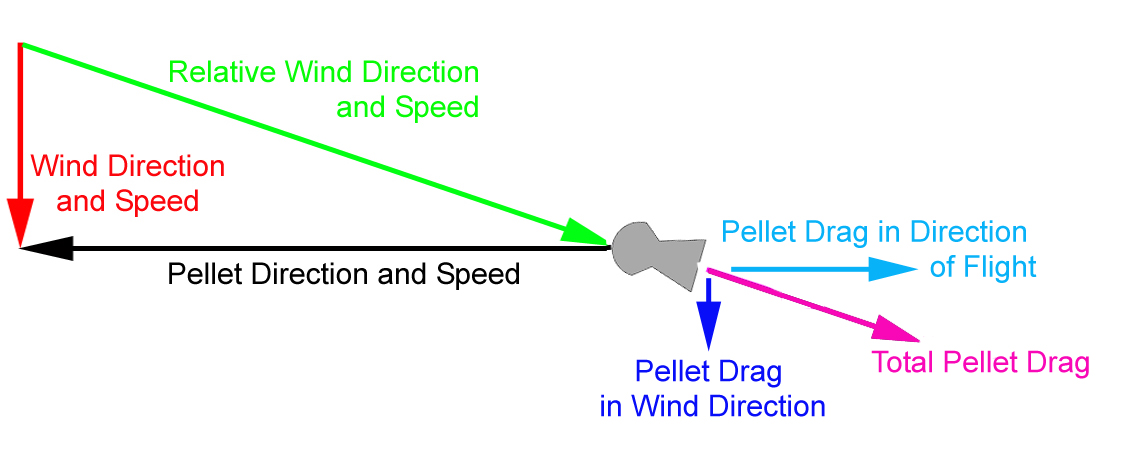
It all comes about because the pellet is not actually pointing in the direction in which it is travelling, so the drag force is at an angle to the pellet's direction of travel, which makes some of the drag act in the direction of the wind. It is this small component of the drag which produces your downwind drift.
But what proof is there that the above is true? From the diagram above, if there is no drag there should be no downwind drift and if the drag is negative then the projectile should drift upwind, not down wind. These effects can be seen with rockets. If a rocket is fired with a motor which exactly equals the drag giving no overall force, a crosswind has no effect on it, whereas an accelerating rocket can be seen to drift upwind. Projectiles fired at the same speed and weight but with different drags have also been shown to have downwind drift proportional to the drag, so the theory is well proven.
While the drag provides the force for the downwind drift, the pellet weight will decide on the acceleration rate of the sideways velocity, producing the rate of the downwind drift. This is where BC becomes useful, as it combines a factor for the pellet drag with the pellet weight. The BC also determines how much the pellet will slow down, and thus contributes to the time difference we looked at before.
The other factor which will determine what the time difference calculated above will be is the pellet velocity. The velocity will affect the size of the drag force as well as the time taken to reach the range of interest.
When a pellet is fired in the air, as everyone knows, it slows down. To reach a certain range from the gun, because it slows down, it will take longer to reach that range than it would have done if it had just kept on going at the same speed. Because the pellet starts to slow down almost immediately after it has left the barrel, it will always take longer to travel a certain range, no matter how large or small the chosen distance is.
Suppose we choose a fixed range, say 30 yards, and a .22 pellet with a muzzle velocity of 585ft/sec. To reach 30 yards, that pellet will take 0.1635 seconds (AA Field pellet). Now if that pellet did not slow down at all but just kept on going at the same speed it would take 0.1538 seconds to travel 30 yards, so we can say that in the air it takes 0.0097 seconds longer to travel 30 yards than it would have done if it had kept going at the same speed. This time difference, the 0.0097 seconds, is called the lag time. The downwind drift at 30 yards for our pellet fired in the air is then given by the cross wind speed multiplied by that time difference. So in our case, for a 5mph cross wind, which is the same as a 88inches/sec cross wind, the downwind drift will be 0.0097 X 88 which comes out to 0.8536 inches. But the question is, why is downwind drift dependent on how much the pellet slows down?
The most popular misconception is that a crosswind blows on the side of a pellet. It is not surprising that this myth is popular, before now I have seen it written down in magazines, stated in videos and on forums. The wind will not blow on the side of the pellet if the pellet is stable (unless the pellet is grossly gyroscopically over stable, in which case you will have much more than a cross wind to worry about). A stable pellet, by definition, will always turn to face the direction from which the air is coming when it meets the front of the pellet. If there is no cross wind, the only thing giving a direction for the air to come from is the pellets own speed as it moves through the air, so the pellet will face in that direction.
When there is a cross wind, the air direction is not just due to the pellet speed. There is also the wind speed to think of. The pellet though does not see two separate wind directions, it sees a combination of the directions of the cross wind speed and the wind speed from the pellets own movement creating a relative airflow. Again, by the definition of a stable pellet, the pellet will turn to face the direction of the relative air flow from the cross wind and the pellet speed. The diagram below shows what is happening.
If the pellet is facing into the combined relative airflow, then there cannot be any flow on the side of the pellet to push it sideways down wind.
Since the pellet is facing the airflow, the only force acting on it is drag, and it is part of the drag force which produces the downwind drift. The next diagram shows how this happens.
It all comes about because the pellet is not actually pointing in the direction in which it is travelling, so the drag force is at an angle to the pellet's direction of travel, which makes some of the drag act in the direction of the wind. It is this small component of the drag which produces your downwind drift.
But what proof is there that the above is true? From the diagram above, if there is no drag there should be no downwind drift and if the drag is negative then the projectile should drift upwind, not down wind. These effects can be seen with rockets. If a rocket is fired with a motor which exactly equals the drag giving no overall force, a crosswind has no effect on it, whereas an accelerating rocket can be seen to drift upwind. Projectiles fired at the same speed and weight but with different drags have also been shown to have downwind drift proportional to the drag, so the theory is well proven.
While the drag provides the force for the downwind drift, the pellet weight will decide on the acceleration rate of the sideways velocity, producing the rate of the downwind drift. This is where BC becomes useful, as it combines a factor for the pellet drag with the pellet weight. The BC also determines how much the pellet will slow down, and thus contributes to the time difference we looked at before.
The other factor which will determine what the time difference calculated above will be is the pellet velocity. The velocity will affect the size of the drag force as well as the time taken to reach the range of interest.
Last edited: